2360. 图中的最长环(困难)

Posted on In Views:

1，问题描述

2360. 图中的最长环

难度：困难

给你一个 n 个节点的 有向图 ，节点编号为 0 到 n - 1 ，其中每个节点 至多 有一条出边。

图用一个大小为 n 下标从 0 开始的数组 edges 表示，节点 i 到节点 edges[i] 之间有一条有向边。如果节点 i 没有出边，那么 edges[i] == -1 。

请你返回图中的 最长 环，如果没有任何环，请返回 -1 。

一个环指的是起点和终点是 同一个 节点的路径。

示例 1：

img

1
2
3
4
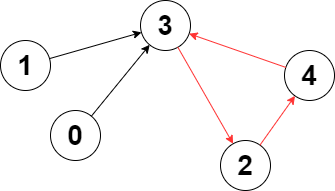
输入：edges = [3,3,4,2,3]
输出去：3
解释：图中的最长环是：2 -> 4 -> 3 -> 2 。
这个环的长度为 3 ，所以返回 3 。

示例 2：

img

1
2
3
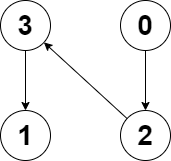
输入：edges = [2,-1,3,1]
输出：-1
解释：图中没有任何环。

提示：

  • n == edges.length
  • 2 <= n <= 105
  • -1 <= edges[i] < n
  • edges[i] != i

2，初步思考

​ 直接进行遍历即可

3，代码处理

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
package questions;

import java.util.HashMap;
import java.util.Map;

public class _2360图中的最长环 {
    public int longestCycle_optimize_v2(int[] edges) {
        int n = edges.length, max = -1, curTime = 1; // 当前时间
        int[] visTime = new int[n];
        for (int i = 0; i < n; i++) {
            int idx = i;// 起点
            int startTime = curTime; // 本轮循环的开始时间
            while (idx != -1 && visTime[idx] == 0) {
                visTime[idx] = curTime++;
                idx = edges[idx];
            }
            if (idx != -1 && visTime[idx] >= startTime) {
                max = Math.max(max, curTime - visTime[idx]);
            }
        }

        // 2,返回结果
        return max == 0 ? -1 : max;
    }


    // 解法优化
    public int longestCycle_optimize(int[] edges) {
        int n = edges.length;
        int[] cntList = new int[n];
        int max = -1;
        for (int i = 0; i < n; i++) {
            int idx = edges[i];
            if (idx != -1) {
                cntList[idx]++;
            }
        }

        // 2,遍历所有节点，判断是否是环
        int[] cntListCur;
        for (int i = 0; i < n; i++) {
            if (cntList[i] > 0) {
                int idx = i;// 起点
                cntListCur = new int[n];
                int cntCur = 0;
                while (idx != -1 && cntListCur[idx] == 0 && cntList[idx] > 0) {
                    cntCur++;
                    cntListCur[idx] = cntCur;
                    cntList[idx]--;
                    idx = edges[idx];
                }
                if (idx != -1 && cntListCur[idx] > 0) {
                    max = Math.max(max, cntCur - cntListCur[idx] + 1);
                }
            }
        }

        // 3,返回结果
        return max == 0 ? -1 : max;
    }

    // 解法：遍历所有节点，判断是否是环
    public int longestCycle(int[] edges) {
        // 1,缓存被指向次数大于等于1的节点
        int n = edges.length;
        int[] cntList = new int[n];
        int max = -1;
        for (int i = 0; i < n; i++) {
            int idx = edges[i];
            if (idx != -1) {
                cntList[idx]++;
            }
        }

        for (int i = 0; i < n; i++) {
            if (cntList[i] > 0) {
                int idx = i;// 起点
                Map<Integer, Integer> mapCur = new HashMap<>();
                while (idx != -1 && cntList[idx] > 0 && !mapCur.containsKey(edges[idx])) {
                    mapCur.put(idx, mapCur.size());
                    cntList[idx]--;
                    idx = edges[idx];
                }
                if (idx != -1 && mapCur.containsKey(edges[idx])) {
                    max = Math.max(max, mapCur.size() - mapCur.get(edges[idx]) + 1);
                }
            }
        }

        // 3,返回结果
        return max == 0 ? -1 : max;
    }

    public static void main(String[] args) {
        _2360图中的最长环 longestCycle = new _2360图中的最长环();
//        System.out.println(longestCycle.longestCycle_optimize_v2(new int[]{3, 3, 4, 2, 3}));
        System.out.println(longestCycle.longestCycle_optimize_v2(new int[]{3, 4, 0, 2, -1, 2}));
//        System.out.println(longestCycle.longestCycle_optimize_v2(new int[]{-1, 4, -1, 2, 0, 4}));
//        System.out.println(longestCycle.longestCycle(new int[]{2, -1, 3, 1}));
//        System.out.println(longestCycle.longestCycle(new int[]{
//                22, 42, -1, 6, 48, 3, 16, 44, 44, 34,
//                18, -1, 39, 10, 34, 48, 13, 16, 47, 22,
//                -1, 39, 14, 20, -1, -1, 24, 48, 35, 26,
//                43, -1, 48, 48, 7, 37, 12, 34, -1, 43,
//                15, -1, 47, 13, 39, 3, 16, 22, 0, 7, 46}));
    }
}